Voilà une note écrite le 6 septembre 2000 sur les mesures de la croissance. Les chiffres sont un peu anciens (et en francs dans le cas de la France) mais ils permettent de faire des calculs simples.
Un de mes correspondants m’a interrogé sur les notions d’acquis de croissance, de contribution à la croissance… L’objet de ce post est de faire un rapide point sur ces outils utilisés par les économistes pour appréhender la conjoncture. Ils vous permettront de bien discriminer les propos des économistes.
LA CROISSANCE
Il existe différentes mesures d’évolution d’un même indicateur d’activité. Ici on prendra le PIB en volume comme indicateur de l’activité. C’est la mesure la plus large de celle ci et c’est le PIB qui est utilisé pour mesurer la croissance.
En général, dans les présentations, la notion de croissance dont il est question est la croissance moyenne. La croissance française a été de 2.9 % en 1999. Cela signifie que le PIB moyen de 1999 a progressé de 2.9 % par rapport au PIB moyen de 1998.
On calcule également la croissance en glissement annuel qui est le taux de croissance entre le PIB d’un trimestre donné et le PIB du même trimestre de l’année précédente.
Techniquement on appelle Y1,99, Y2,99, Y3,99, et Y4,99 le PIB en niveau des quatre trimestres de l’année 1999. On adoptera les mêmes notations pour les autres années.
Calcul de la croissance moyenne
On fait la moyenne des 4 trimestres d’une même année
Y99 = (Y1,99 + Y2,99 + Y3,99 + Y4,99 ) / 4
On effectue le même calcul pour 1998 et l’on obtient Y98.
Le taux de croissance moyen sera
Cm = (Y99 – Y98) / Y98
Calcul de la croissance en glissement
Cg = (Y4,99 – Y4,98) / Y4,98
Les deux modes de calcul n’ont a priori pas le même résultat.
Prenons deux exemples.
Au Japon, la croissance moyenne en 1999 a été de 0.27 %. La croissance en glissement entre le quatrième trimestre de 1998 et le quatrième trimestre de 1999 a été de –0.19 %.
Sur le graphique plus bas on note effectivement que la moyenne 99 est légèrement supérieure à la moyenne, d’où le chiffre positif de la croissance moyenne. En revanche le point du dernier trimestre de 1999 est au-dessous de celui du dernier trimestre de 1998 d’où le chiffre négatif de la croissance en glissement.
Dans le cas des Etats-Unis, la configuration est radicalement différente. La croissance moyenne a été de 4.23 % alors que la croissance en glissement a été de 4.96 %. On voit bien sur le graphe ci-dessous que les chiffres de 1999 sont au-dessus de ceux de 1998 que ce soit pour la moyenne ou pour le dernier trimestre de 1999 très supérieur à celui du dernier trimestre 1998.
L’intérêt de ces deux mesures est d’affiner le diagnostic conjoncturel. Dans le cas du Japon, on perçoit que la mesure moyenne donne une image un peu faussée de la dynamique conjoncturelle notamment sur la fin de l’année.
Aux USA, la hiérarchie des taux de croissance montre que l’économie a accéléré en cours d’année et peut laisser supposer une accélération au cours du second semestre.
Les graphiques ci dessous montrent les dynamiques très différenciées entre ces deux économies.
Le taux de croissance annualisé
Pour présenter la croissance du PIB d’un trimestre sur l’autre, les statisticiens américains l’expriment en taux de croissance annualisé (c’est à dire en prenant la puissance 4 de la variation simple) alors que les européens l’expriment davantage en taux de croissance simple.
Le calcul est le suivant (en reprenant les mêmes notations).
Taux de croissance simple = (Y2,00 – Y1,00) / Y1,00 = (Y2,00 / Y1,00) – 1
Taux de croissance annualisé = [(Y2,00 / Y1,00)4] – 1
Le taux de croissance annualisé permet de comparer directement un taux de croissance annuel en glissement (comme calculé précédemment) à un taux de croissance trimestriel. En effet le taux de croissance annualisé permet de calculer ce que serait la croissance annuelle si le taux de croissance simple se répétait à chaque trimestre sur un an.
L’acquis de croissance
Lorsqu’un chiffre du PIB sort, on calcule très rapidement l’acquis de croissance. Il s’agit d’un calcul simple qui est à relier au calcul de la croissance moyenne.
Supposons que soit publié le chiffre du PIB du 4eme trimestre. L’acquis (de croissance) est le calcul qui permet de trouver le taux de croissance moyen de l’année suivante si le niveau d’activité restait au niveau du 4eme trimestre. (la moyenne de l’année suivante est égale au niveau du 4eme trimestre de l’année courante)
L’acquis à la fin de l’année 1999 est ainsi le suivant :
Acquis = (Y4,99 – Y99) / Y99
Pour reprendre les deux exemples précédents, on note que le PIB japonais au dernier trimestre de 1999 est très inférieur à sa moyenne. L’acquis est de –1.50%. Cela signifie que si l’activité restait au niveau du dernier trimestre de 99, la croissance moyenne en 2000 serait de –1.50 %. Cela implique également que le point de départ étant très bas, la croissance japonaise aura du mal en 2000 à être très forte en moyenne (même si par exemple elle progressait très fortement en glissement).
Dans le cas américain, l’acquis est de 2.35 %. Si l’activité était restée au niveau du dernier trimestre de 99, la croissance moyenne US aurait été de 2.35 %. Tout accroissement de l’activité s’ajoute à ces 2.35 %.
Cette notion est donc importante dans le calcul de la croissance moyenne lorsque l’on fait des prévisions.
Par extension, on peut calculer l’acquis à la fin de n’importe quel trimestre en faisant l’hypothèse que l’activité se maintiendra au niveau du dernier trimestre connu jusqu’à la fin de l’année. Dans le cas américain par exemple, on connaît le chiffre du deuxième trimestre Y2,00.
L’acquis de croissance est de supposer qu’aux troisième et quatrième trimestres, l’activité restera au niveau de Y2,00 pour calculer un taux de croissance moyen.
Le calcul est alors le suivant :
Si l’on note Ym2,00 le PIB moyen en 2000 en supposant que Y3,00 = Y4,00 = Y2,00 soit
Ym2,00 = (Y1,00 + Y2,00 + Y2,00 + Y2,00) / 4
L’acquis de croissance à la fin du deuxième trimestre = (Ym2,00 – Y99) / Y99
Dans le cas américain, l’acquis est de 4.57 %. Si l’activité aux troisième et quatrième trimestres de 2000 restait au niveau du deuxième trimestre, la croissance moyenne américaine serait de 4.57 % en 2000.
Les contributions a la croissance
Lorsque l’on a un chiffre de PIB, il est intéressant de savoir de quel poste provient la croissance: c’est l’analyse des contributions.
Partons d’un schéma simple.
L’équilibre de l’activité traduit des effets de demande et d’offre.
La demande regroupe : la consommation des ménages (que l’on notera C), l’investissement (I) (des entreprises et en logement), les dépenses gouvernementales (G), les exportations (X) et les variations de stocks (S).
L’offre regroupe : le PIB (Y) (c’est la production) et les importations (M).
L’offre égale la demande puisque les produits offerts se répartissent en consommation, investissement etc…
On obtient donc
Y + M = C + I + G + X + S
Offre = Demande
A la date 1 on a
(1) Y1 + M1 = C1 + I1 + G1 + X1 + S1
A la date 2 on a
(2) Y2 + M2 = C2 + I2 + G2 + X2 + S2
Si l’on soustrait on (1) de (2) on obtient
Y2 – Y1 + M2 – M1 = C2 – C1 + I2 – I1 + G2 – G1 + X2 – X1 + S2 – S1
En divisant par Y1 on obtient
(Y2 – Y1)/ Y1 + (M2 – M1)/ Y1 = (C2 – C1)/ Y1+(I2 – I1)/ Y1+(G2 – G1)/ Y1+(X2 – X1)/ Y1+ (S2 – S1)/ Y1
Après on peut s’apercevoir que (Z2 – Z1) / Y1 = [(Z2 – Z1)/Z1] * Z1/Y1 = z*Z1/Y1
Où z est le taux de croissance de la variable Z quelconque entre la période 1 et la période 2 et Z1/Y1 est la proportion de Z dans le PIB (Y) à la période 1.
On a donc :
(3) y + m* M1/Y1 = c*C1/Y1 + i*I1/Y1 + g*G1/Y1 + x*X1/Y1 + Ajustement des stocks
cela peut se réécrire
(4) y = c*C1/Y1 + i*I1/Y1 + g*G1/Y1 + (x*X1/Y1 – m*M1/Y1) + Ajust. des stocks
La croissance du PIB (y) est donc une moyenne pondérée des différentes composantes. On en déduit la contribution de la consommation comme étant égale à : c*C1/Y1, celle de l’investissement vaut : i*I1/Y1 etc…..
La contribution de la demande interne est égale à la somme des contributions des composantes de la demande interne soit
Contrib.Dem.Int. = c*C1/Y1 + i*I1/Y1 + g*G1/Y1
La contribution des échanges extérieurs est égale à
Contrib.Dem.Ext = x*X1/Y1 – m*M1/Y1
Exemple sur le cas français à partir du chiffre du PIB du deuxième trimestre
Prenons les chiffres du premier trimestre 1998 au 2ème trimestre 2000 (compte tenu des révisions et changements de base, les chiffres actuels ne ressemblent plus à ceux-là. L’exemple est présenté à titre heuristique.
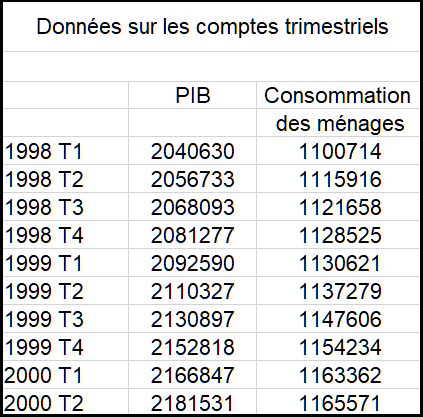
Les chiffres présentés ci contre sont un extrait des comptes trimestriels. Ils sont exprimés en millions de francs 1995.
Calcul de la croissance moyenne 99/98
Y99 = (2092590+2110327+2130897+2152818)/4
= 2121658
Y98 = (2040630+2056733+2068093+2081277
= 2061683.25
Cm = (2121658 – 2061683.25)/2061683.25
= 0.0290
soit Cm = 2.9 %
Calcul de la croissance en glissement
Cg = (2152818-2081277)/2081277 = 0.03437
Soit Cg = 3.44 %.
Calcul de l’acquis à la fin de l’année 99
En reprenant la formule du texte on a :
Acquis = (Y4,99 – Y99) / Y99 = (2152818-2121658)/2121658 = 0.01468
Soit Acquis = 1.47 %
Calcul de l’acquis à la fin du second trimestre
En reprenant les notations du texte on a
Ym00 = (2166847+2181531+2181531+2181531)/4 = 2177860
Acquis = (Ym00 – Y99)/Y99 = (2177860 – 2121658)/2121658 = 0.02649
Soit Acquis = 2.65 %
Calcul de la contribution trimestrielle de la consommation
La croissance de la consommation au deuxième trimestre de 2000 a été de
Cc = (1165571-1163362)/1163362 = 0.00189 = 0.2 %
Le calcul en taux annualisé aurait donné
Cac = ((1165571/1163362)4)-1 = 0.0076 = 0.76 %
La contribution trimestrielle = 0.2 * (1163362/2166847) = 0.10 %
La contribution trimestrielle en taux annualisé = 0.76 * (1163362/2166847) = 0.41 %
Calcul de la contribution annuelle de la consommation
La croissance en glissement annuel de la consommation au deuxième trimestre de 2000 a été de
Cgc = (1165571-1137279)/1137279 = 0.0248 = 2.48 %
La contribution annuelle = 2.48 * (1137279/2110327) = 1.34 %
On peut effectuer les mêmes calculs pour les autres postes de la demande.
.





